6. ΜΕΛΕΤΗ ΣΥΝΑΡΤΗΣΕΩΝ  y = α + β x+ γ

    Kατασκευάzουμε ένα πίνακα τιμών για διάφορες τιμές του συντελεστή διεύθυνσης α, ειδικότερα για α = 0, 2, -2, 4, -4:

    Σχεδιάζουμε τις συναρτήσεις f(x) = α , για α = -2 (1) 2, όπως ακολουθεί:

    Τι συμπεράσματα μπορούμε να βγάλουμε από τις παραπάνω γραφικές παραστάσεις για τη συνάρτηση f(x) = α σχετικά:
    1) με την κορυφή;
    
    
    2) με τη μονοτονία;
    
    
    3) τα ακρότατα;
    
    
    4) τις συμμετρίες;  
    
    
    5) τα σημεία τομής με τους άξονες;
    
    

    Θεωρούμε τη συνάρτηση f(x)= α + β.
    Σχεδιάζουμε τη γραφική παράσταση της f(x)=-2 + β, για β = -3 (1) 3 βήμα βήμα:

    Τι συμπεράσματα μπορούμε να βγάλουμε από τις παραπάνω γραφικές παραστάσεις για τη συνάρτηση f(x) = α + β σχετικά:
    1) με την κορυφή;
    
    
    2) με τη μονοτονία;
    
    
    3) τα ακρότατα;
    
    
    4) τις συμμετρίες;  
    
    
    5) τα σημεία τομής με τους άξονες;
    
    

    Θεωρούμε τη συνάρτηση f(x)= α.
    Σχεδιάζουμε τη γραφική παράσταση της f(x)= 2 , για κ = -10 (2) 10 βήμα βήμα:

    Τι συμπεράσματα μπορούμε να βγάλουμε από τις παραπάνω γραφικές παραστάσεις για τη συνάρτηση f(x) = α σχετικά:
    1) με την κορυφή;
    
    
    2) με τη μονοτονία;
    
    
    3) τα ακρότατα;
    
    
    4) τις συμμετρίες;  
    
    
    5) τα σημεία τομής με τους άξονες;
    
    

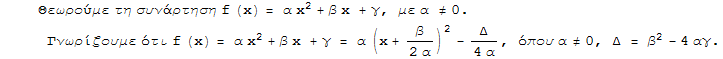
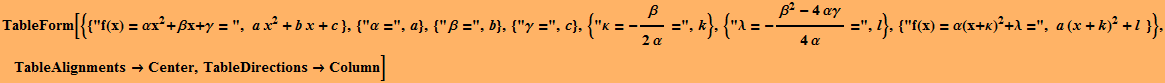
α =	-2
β =	8
γ =	3
	2
	11

    Τι συμπεράσματα μπορούμε να βγάλουμε από τις παραπάνω γραφικές παραστάσεις για τη συνάρτηση f(x)= α +β x +γ = α-, όπου α≠0, Δ = -4αγ.
    1) με την κορυφή;
    
    
    2) με τη μονοτονία;
    
    
    3) τα ακρότατα;
    
    
    4) τις συμμετρίες;  
    
    
    5) τα σημεία τομής με τους άξονες;
    
    
    

Βιβλιογραφία:
1) Κορρές Κ. (2003). Η χρήση του Η/Υ ως γνωστικού εργαλείου στη διδασκαλία των μαθηματικών. Πρακτικά του 20ου Πανελλήνιου Συνεδρίου Μαθηματικής Παιδείας της Ελληνικής Μαθηματικής Εταιρείας, με τίτλο «Η διαδρομή του παιδιού από την προσχολική ηλικία μέχρι την ενηλικίωση». Βέροια, 7 - 9 Νοεμβρίου 2003.
2) Kyriazis A. & Korres K. (2002). Teaching Linear Functions in Junior High School, with the use of Computers. Proceedings of the 3rd Hellenic Conference with International participation, of the Hellenic Scientific Association of Information & Communication Technologies in Education (ETPE).
3) Κυριαζής Α. & Κορρές Κ. (2001). Θέματα Δευτεροβάθμιας Εκπαίδευσης: Μελέτη θεμάτων με τη βοήθεια του Mathematica®. Σημειώσεις επιμόρφωσης στα πλαίσια του επιμορφωτικού προγράμματος ετήσιας διάρκειας, για τους εκπαιδευτικούς Μαθηματικούς», για το μάθημα «Νέες Τεχνολογίες στην Εκπαίδευση», με διδάσκοντα τον κ. Α. Κυριαζή, Καθηγητή. Τμήμα Μαθηματικών, Πανεπιστήμιο Αθηνών.

Created by Mathematica  (November 4, 2015)